I present for your amusement and/or scorn, a variety of weirdo mechanics to look over and/or try in your fifth edition Dungeons & Dragon game, or any other dice game that they might fit into. Someday I’ll make a Patreon and store these in a PDF there.

Mid-vantage: For when you want things to be dull and disappointing but not entirely defeatist, roll three dice and discard the highest and lowest dice (keeping ties, obviously).

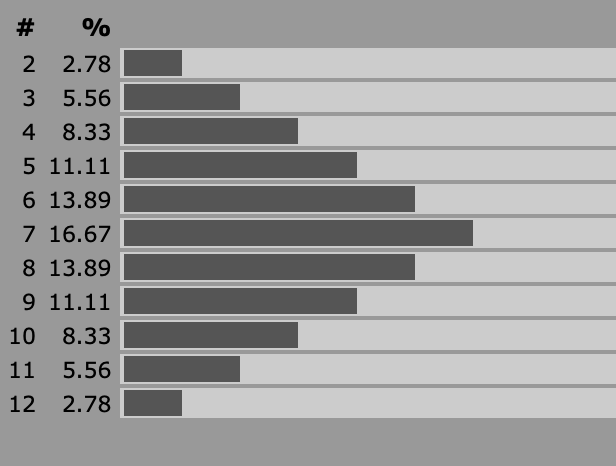
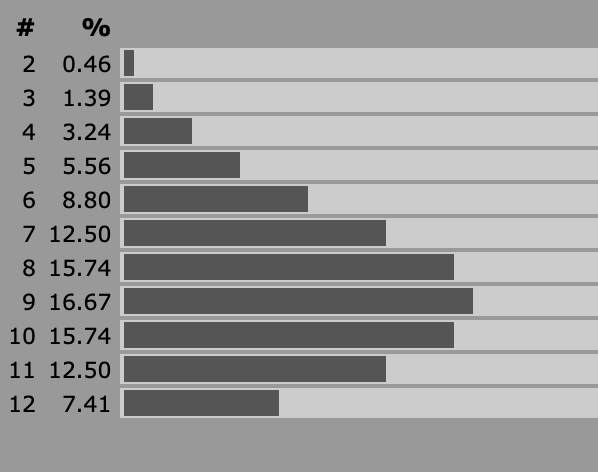
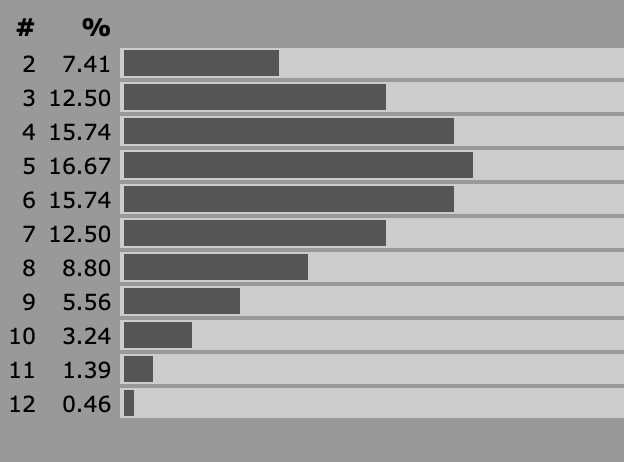
Roll 3d6, keep the high/low two: This is useful for when you have something like a random encounter table that you want to be situationally dependent without ruling out certain values like adding a straight +/- modifier would. It doesn’t have to be a 2d6 table, that’s just nicely illustrative of the effect. The probability curve doesn’t just shift, it also ends up weighted more in the direction of the shift. Handy for when the party is really due to meet a wizard or a dragon.

Shaking up chases: I started writing this up, but it had spiraled into multiple paragraphs and wailing despair, so I rolled it over into a separate draft for another time.

Phased HP exhaustion: If you want more than the last hit point to matter, and if you want your bastard PCs to suffer before they die, they can acquire exhaustion as they lose HP. The ordinary sequence of exhaustion is 1) Disadvantage on ability checks, 2) Speed halved, 3) Disadvantage on attack rolls and saving throws, 4) Hit point maximum halved, 5) Speed reduced to 0, and 6) Death. Death at 0 hit points isn’t very helpful, so if we leave death at negative max HP or three failed death saves (whichever comes first) then we have five nice levels to apply to our characters’ dwindling hit points. Bob the Barbarian (Path of the Death Spiral) has 40 hit points. We divide these up into twenty percent chunks and then give Bob a level of exhaustion for each threshold he passes. When Bob’s hit points are from 32-39, he has one level of exhaustion and disadvantage on ability checks. 24-31, two levels and now his speed is halved in addition to the previous effect. 16-23, disadvantage on attack rolls and saving throws piles on and Bob is really suffering. 8-15, Bob can’t heal past half of his maximum hit points until he shakes this off, and from 1-7 the poor fellow can’t even move. Die, you bastard!

Of course, this is fiddly and brutal and will throw the game wildly out of whack, but it seems like nasty fun if your characters ever visit somewhere like the Plane of Sleepless Infant Parenting.

Mass combat, part 1: No matter how many times I’m told it isn’t needed, I still acutely feel the absence of a decent mass combat system in 5e. It’s a project that I’ve rolled over in my head for years and I intend to tackle it in full at some point in the relatively near future. But for now, here’s a related system I’ve used to quickly resolve less-important combat in order to keep the focus of the game on the players and their direct opponents. I came up with it for the adventure I wrote for GameholdCon in 2023. There is the possibility of an unwieldy battle between multiple demons and devils at the climax of the adventure, and rather than have the DM roll piles of dice while the other players watch and wait, I came up with a matrix to present the average damage each fiend would do against each of its potential opponents. The DM could just look up the expected damage, apply it, and move on. The full matrix was needed in order to incorporate armor class and to hit bonuses, multiple attacks, resistances, and so on. Fun fact: demons and devils are resistant or immune to most of each other’s attacks, so the Blood War really looks like an interminable slap slog.

On to the formula! Let’s say Bob the Barbarian has had a week’s rest and shed all of that nasty exhaustion, but while he’s fighting someone important, three hill giants are bashing his hireling Helga back and forth. So many dice for a monster vs NPC fight, so little time. We’re going to take the individual hill giant’s to hit modifier (+8) and average damage (18) and Helga’s AC (let’s say, 14) and plug them into this formula: .05(to hit +21 -AC)*dmg. We get .05(8+21-14)*18. The most important part of that is .05(8+21-14) which equals .75 because a hill giant is going to hit AC 14 75% of the time. Therefore, our many hill giants don’t deal average damage with every attack, they deal 75% of average damage against Helga’s AC with every attack (so long, Helga!).

I might be a little off, but I haven’t had the best sleep for the last couple of weeks, so tell me if I’m wrong as nicely as you can. I’m going to keep playing with this and see if I can expand it into a system that can handle large scale battles in a quick and satisfying manner. Dice are bound to re-enter the equation at some point, so don’t expect it consist entirely of proportional damage numbers being smashed against each other. In the meantime, for a proper and impressive examination of 5e math, check out the Finished Book by Tom Dunn.